exercises
Question 3.98
Let \(f(x, y)=x^2+3y^2\). Find the maximum and minimum values of \(f\) subject to the given constraint.
- (a) \( x^2+y^2=1\)
- (b) \( x^2+y^2 \leq 1\)
Question 3.99
Consider all rectangles with fixed perimeter \(p\). Use Lagrange multipliers to show that the rectangle with maximal area is a square.
In Exercises 3 to 7, find the extrema of f subject to the stated constraints.
Question 3.100
\(f(x,y,z) = x-y +z\), subject to \(x^2 + y^2 + z^2 = 2\)
Question 3.101
\(f(x,y) = x- y\), subject to \(x^2 - y^2 = 2\)
Question 3.102
\(f(x,y) = x\), subject to \(x^2 + 2y^2 = 3\)
Question 3.103
\(f(x, y, z) = x+ y + z\), subject to \(x^2 - y^2 = 1, 2x + z =1\)
Question 3.104
\(f(x,y) = 3x + 2y\), subject to \(2x^2 + 3y^2 =3\)
Find the relative extrema of \(f{\mid} S\) in Exercises 8 to 11.
Question 3.105
\(f{:}\,\, {\mathbb R}^2 \rightarrow {\mathbb R}, (x,y) \mapsto x^2 + y^2, S = \{(x,2) \mid x \in {\mathbb R} \}\)
Question 3.106
\(f{:}\,\, {\mathbb R}^2 \rightarrow {\mathbb R}, (x,y) \mapsto x^2 + y^2, S = \{(x,y) \mid y \geq 2 \}\)
Question 3.107
\(f{:}\,\, {\mathbb R}^2 \rightarrow {\mathbb R}, (x,y) \mapsto x^2 - y^2, S = \{(x,\cos x) \mid x \in {\mathbb R} \}\)
Question 3.108
\(f{:}\,\, {\mathbb R}^3 \rightarrow {\mathbb R}, (x,y,z) \mapsto x^2 + y^2 + z^2, S = \{(x,y,z) \mid z \geq 2 + x^2 + y^2 \}\)
Question 3.109
Use the method of Lagrange multipliers to find the absolute maximum and minimum values of \(f(x,y) = x^2 + y^2 -x - y +1\) on the unit disc (see Example 10 of Section 3.3).
Question 3.110
Consider the function \(f(x,y) = x^2 + xy + y^2\) defined on the unit disc, namely, \(D = \{(x,y) \mid x^2 + y^2 \leq 1\}\). Use the method of Lagrange multipliers to locate the maximum and minimum points for \(f\) on the unit circle. Use this to determine the absolute maximum and minimum values for \(f\) on \(D\).
202
Question 3.111
Find the absolute maximum and minimum values of \(f(x, y, z)=2x+y\), subject to the constraint \(x+y+z=1\).
Question 3.112
Find the extrema of \(f(x, y)=4x+2y\), subject to the constraint \(2x^2+3y^2=21\).
Question 3.113
Use Lagrange multipliers to find the distance from the point (2, 0, \(-1\)) to the plane \(3x-2y+8z+1=0\). Compare your answer to Example 12 in Section 1.3.
Question 3.114
Find the maximum and minimum values attained by \(f(x, y, z)=xyz\) on the unit ball \(x^2+y^2+z^2 \leq 1\).
Question 3.115
Let \(S\) be the sphere of radius 1 centered at (1, 2, 3). Find the distance from \(S\) to the plane \(x+y+z=0\). (HINT: Use Lagrange multipliers to find the distance from the plane to the center of the sphere.)
Question 3.116
- (a) Find three numbers whose product is 27 and whose sum is minimal.
- (b) Find three numbers whose sum is 27 and whose product is maximal.
Question 3.117
A rectangular box with no top is to have a surface area of 16 m\(^2\). Find the dimensions that maximize its volume.
Question 3.118
Design a cylindrical can (with a lid) to contain 1 liter (\({=}\,\)1000 cm\(^{3}\)) of water, using the minimum amount of metal.
Question 3.119
Show that solutions of equations (4) and (5) are in one-to-one correspondence with the critical points of \begin{eqnarray*} && h(x_1,\ldots, x_n, \lambda_1, \ldots, \lambda_k) \\ &&\quad = f(x_1, \ldots,x_n) -\lambda_1 [g_1(x_1,\ldots,x_n)\,{-}\,c_1]\\ &&\quad - \cdots - \lambda_k [g_k(x_1,\ldots,x_n)-c_k]. \end{eqnarray*}
Question 3.120
Find the absolute maximum and minimum for the function \(f(x,y,z)=x+y-z\) on the ball \(B=\{(x,y,z)\mid x^2+y^2+z^2\leq 1\}\).
Question 3.121
Repeat Exercise 23 for \(f(x,y,z)=x+yz\).
Question 3.122
A rectangular mirror with area \(A\) square feet is to have trim along the edges. If the trim along the horizontal edges costs \(p\) cents per foot and that for the vertical edges costs \(q\) cents per foot, find the dimensions that will minimize the total cost.
Question 3.123
An irrigation canal in Arizona has concrete sides and bottom with trapezoidal cross section of area \(A=y(x + y \tan \theta)\) and wetted perimeter \(P=x + 2y/ \cos \theta\), where \(x=\) bottom width, \(y=\) water depth, and \(\theta =\) side inclination, measured from vertical. The best design for a fixed inclination \(\theta\) is found by solving \(P=\) minimum subject to the condition \(A = \hbox{constant}\). Show that \(y^2 = (A \cos \theta)/(2 - \sin \theta)\).
Question 3.124
Apply the second-derivative test to study the nature of the extrema in Exercises 3 and 7.
Question 3.125
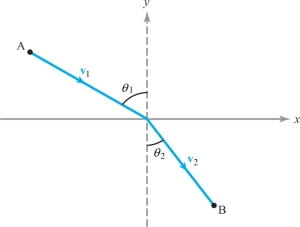
A light ray travels from point A to point B crossing a boundary between two media (see Figure 3.20). In the first medium its speed is \(v_1\), and in the second it is \(v_2\). Show that the trip is made in minimum time when Snell’s law holds: \[ \frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2}. \]
Question 3.126
A parcel delivery service requires that the dimensions of a rectangular box be such that the length plus twice the width plus twice the height be no more than 108 inches \((l + 2w +\) \(2h \leq 108)\). What is the volume of the largest-volume box the company will deliver?
Question 3.127
Let P be a point on a surface \(S\) in \({\mathbb R}^3\) defined by the equation \(f(x,y,z)=1\), where \(f\) is of class \(C^1\). Suppose that P is a point where the distance from the origin to \(S\) is maximized. Show that the vector emanating from the origin and ending at P is perpendicular to \(S\).
Question 3.128
Let \(A\) be a nonzero symmetric \(3 \times 3\) matrix. Thus, its entries satisfy \(a_{\it ij} = a_{ji}\). Consider the function \(f({\bf x}) = \frac{1}{2} (A{\bf x})\, {\cdot}\, {\bf x}\).
- (a) What is \({\nabla}\! f\)?
- (b) Consider the restriction of \(f\) to the unit sphere \(S = \{(x,y,z) \mid x^2 + y^2 + z^2 = 1\}\) in \({\mathbb R}^3\). By Theorem 7 we know that \(f\) must have a maximum and a minimum on \(S\). Show that there must be an \({\bf x}\in S\) and a \(\lambda \neq 0\) such that \(A{\bf x} = \lambda{\bf x}.\) (The vector \({\bf x}\) is called an eigenvector, while the scalar \(\lambda\) is called an eigenvalue.)
- (c) What are the maxima and minima for \(f\) on \(B=\{(x,y,z)\mid x^2+y^2+z^2\leq 1\}\)?
203
Question 3.129
Suppose that \(A\) in the function \(f\) defined in Exercise 31 is not necessarily symmetric.
- (a) What is \({\nabla} \! f\)?
- (b) Can we conclude the existence of an eigenvector and eigenvalues as in Exercise 31?
Question 3.130
- (a) Find the critical points of \(x+y^2\), subject to the constraint \(2x^2 + y^2 = 1\).
- (b) Use the bordered Hessian to classify the critical points.
Question 3.131
Answer the question posed in the last line of Example 9.
Question 3.132
Try to find the extrema of \(xy + yz\) among points satisfying \(xz =1\).
Question 3.133
A company’s production function is \(Q(x,y) = xy\). The cost of production is \(C(x,y) = 2x + 3y\). If this company can spend \(C(x,y) =10\), what is the maximum quantity that can be produced?
Question 3.134
Find the point on the curve \((\cos t, \sin t, \sin (t/2))\) that is farthest from the origin.
Question 3.135
A firm uses wool and cotton fiber to produce cloth. The amount of cloth produced is given by \(Q(x,y) = xy - x - y +1\), where \(x\) is the number of pounds of wool, \(y\) the number of pounds of cotton, \(x>1\), and \(y>1\). If wool costs \(p\) dollars per pound, cotton costs \(q\) dollars per pound, and the firm can spend \(B\) dollars on material, what should the ratio of cotton and wool be to produce the most cloth?
Question 3.136
Carry out the analysis of Example 10 for the production function \(Q(K,L)= AK^{\alpha}L^{1-\alpha} \), where \(A\) and \(\alpha\) are positive constants and \(0 < \alpha < 1\). This is called a Cobb–Douglas production function and is sometimes used as a simple model for the national economy. \(Q\) is then the aggregate output of the economy for a given input of capital and labor.